Lösung zu Aufgabe 3 (Zufallsversuche)
Ein Spielwürfel wird zwei Mal geworfen.
Bestimme die Wahrscheinlichkeit, dass
- keine 6 auftritt.
- nur Zahlen größer als 2 auftreten.
- zwei Mal die 1 auftritt.
Bei dieser Aufgabe ist das Baumdiagramm etwas umfangreicher.
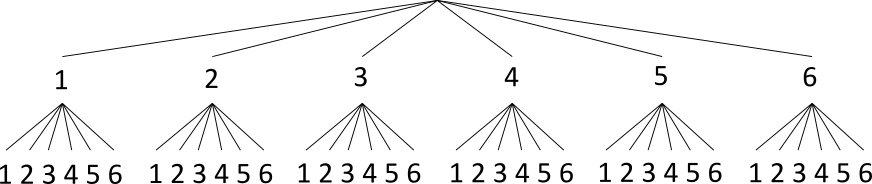
Man kann sich zunutze machen, dass alle Pfadwahrscheinlichkeiten identisch sind. Es ist $p = \frac16$. Weiterhin sind
auch alle Ergebniswahrscheinlichkeiten identisch. Es gilt $P(X) = \frac{1}{36}$.
Für die Bestimmung der Ereigniswahrscheinlichkeiten ist es sinnvoll, das Baumdiagramm zu ergänzen, indem die jeweiligen Ergebnisse, die zu dem Ereignis gehören, markiert werden. Im Anschluss müssen die Ergebnisse nur noch addiert werden.
Die Ereignisse werden wie folgt definiert: \begin{align} E_1 &= \text{ keine } 6 \\ E_2 &= \text{ Zahlen größer als } 2 \\ E_3 &= \text{ zwei Mal } 1 \end{align}
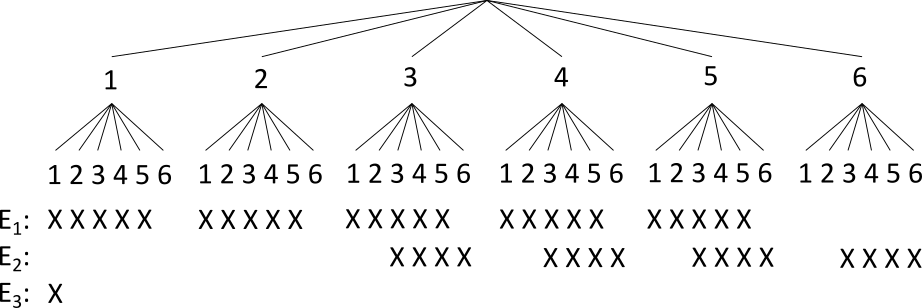
Für das Ereignis $E_1$ sind das 25 Kreuze, für $E_2$ 16 Kreuze und für $E_3$ 1 Kreuz. Damit folgt für die Wahrscheinlichkeiten:
\begin{align}
E_1 &= 25 \cdot \frac{1}{36} = \frac{25}{36} = 0,694 \\
E_2 &= 16 \cdot \frac{1}{36} = \frac{16}{36} = 0,444 \\
E_3 &= 1 \cdot \frac{1}{36} = \frac{1}{36} = 0,028
\end{align}